Papers
My research papers in reverse chronological order. All papers can be found on my arXiv page.
-
 Simulating the quantum switch with quantum circuits is computationally hardJessica Bavaresco, Hlér Kristjánsson, Mio Murao, Tatsuki Odake, Marco Túlio Quintino, Philip Taranto, Satoshi YoshidaNat. Commun. 16, 10216 (2025)
Simulating the quantum switch with quantum circuits is computationally hardJessica Bavaresco, Hlér Kristjánsson, Mio Murao, Tatsuki Odake, Marco Túlio Quintino, Philip Taranto, Satoshi YoshidaNat. Commun. 16, 10216 (2025)Higher-order transformations acting on input quantum channels in an indefinite causal order—such as the quantum switch—cannot be described by quantum circuits using the same number of calls to the input channels. A natural question is whether they can be simulated, i.e., whether their action can be exactly and deterministically reproduced by a quantum circuit with more calls to the input channels. Here, we prove that the quantum switch acting on two n-qubit channels cannot be simulated by any quantum circuit using k calls to one channel and one to the other, if k < 2^n. This establishes an exponential separation in quantum query complexity between processes with indefinite causal order and quantum circuits. Moreover, even with one extra call to both input channels, such a simulation remains impossible. We further demonstrate the robustness of this separation by extending the result to probabilistic and approximate simulations scenarios.
-
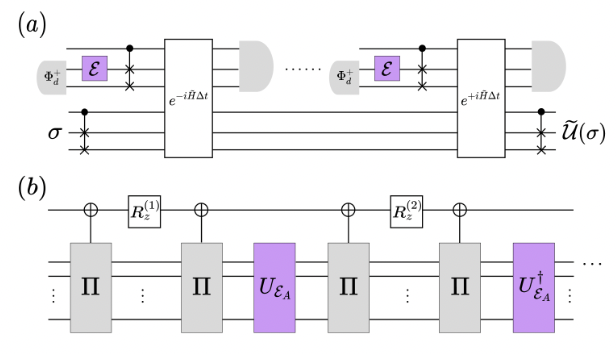 Singular value transformation for unknown quantum channelsRyotaro Niwa, Zane Marius Rossi, Philip Taranto, Mio Murao
Singular value transformation for unknown quantum channelsRyotaro Niwa, Zane Marius Rossi, Philip Taranto, Mio MuraoGiven the ability to apply an unknown quantum channel acting on a d-dimensional system, we develop a quantum algorithm for transforming its singular values. The spectrum of a quantum channel as a superoperator is naturally tied to its Liouville representation, which is in general non-Hermitian. Our key contribution is an approximate block-encoding scheme for this representation in a Hermitized form, given only \emphblack-box access to the channel; this immediately allows us to apply polynomial transformations to the channel’s singular values by quantum singular value transformation (QSVT). We then demonstrate an O(d^3/δ) upper bound and an Ω(d/δ) lower bound for the query complexity of constructing a quantum channel that is δ-close in diamond norm to a block-encoding of the Hermitized Liouville representation. We show our method applies practically to the problem of learning the q-th singular value moments of unknown quantum channels for arbitrary q>2, q∈\mathbbR, which has implications for testing if a quantum channel is entanglement breaking.
-
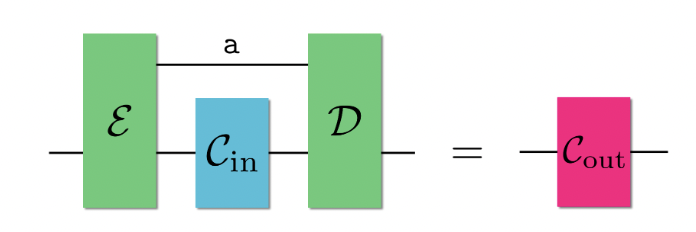 Higher-Order Quantum OperationsPhilip Taranto, Simon Milz, Mio Murao, Marco Túlio Quintino, Kavan Modi
Higher-Order Quantum OperationsPhilip Taranto, Simon Milz, Mio Murao, Marco Túlio Quintino, Kavan ModiAn operational description of quantum phenomena concerns developing models that describe experimentally observed behaviour. Higher-order quantum operations that transform quantum operations are fundamental to modern quantum theory, extending beyond basic state preparations, evolutions, and measurements described by the Born rule. These operations naturally emerge in quantum circuit architectures, correlated open dynamics, and investigations of quantum causality, to name but a few fields of application. This Review Article provides both a pedagogical introduction to the framework of higher-order quantum operations and a comprehensive survey of current literature, illustrated through physical examples. We conclude by identifying open problems and future research directions in this rapidly evolving field.
-
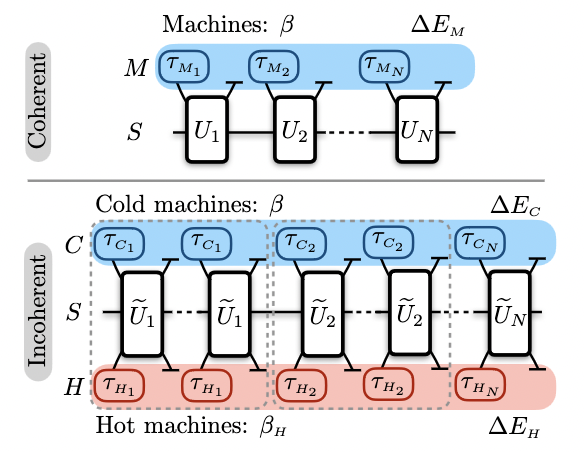 Efficiently Cooling Quantum Systems with Finite Resources: Insights from Thermodynamic GeometryPhilip Taranto, Patryk Lipka-Bartosik, Nayeli A. Rodríguez-Briones, Martí Perarnau-Llobet, Nicolai Friis, Marcus Huber, Pharnam BakhshinezhadPhys. Rev. Lett. 134, 070401 (2025)
Efficiently Cooling Quantum Systems with Finite Resources: Insights from Thermodynamic GeometryPhilip Taranto, Patryk Lipka-Bartosik, Nayeli A. Rodríguez-Briones, Martí Perarnau-Llobet, Nicolai Friis, Marcus Huber, Pharnam BakhshinezhadPhys. Rev. Lett. 134, 070401 (2025)Landauer’s limit on heat dissipation during information erasure is critical as devices shrink, requiring optimal pure-state preparation to minimize errors. However, Nernst’s third law states this demands infinite resources in energy, time, or control complexity. We address the challenge of cooling quantum systems with finite resources. Using Markovian collision models, we explore resource trade-offs and present efficient cooling protocols (that are optimal for qubits) for coherent and incoherent control. Leveraging thermodynamic length, we derive bounds on heat dissipation for swap-based strategies and discuss the limitations of preparing pure states efficiently.
-
 Robust Error Accumulation Suppression for Quantum CircuitsTatsuki Odake, Philip Taranto, Nobuyuki Yoshioka, Toshinari Itoko, Kunal Sharma, Antonio Mezzacapo, Mio MuraoPhys. Rev. Research 7, 033029 (2025)
Robust Error Accumulation Suppression for Quantum CircuitsTatsuki Odake, Philip Taranto, Nobuyuki Yoshioka, Toshinari Itoko, Kunal Sharma, Antonio Mezzacapo, Mio MuraoPhys. Rev. Research 7, 033029 (2025)We present a robust error accumulation suppression (REAS) technique to manage errors in quantum computers. Our method reduces the accumulation of errors in any quantum circuit composed of single- or two-qubit gates expressed as e^-i σθ for Pauli operators 𝜎 and 𝜃∈[0,𝜋), which forms a universal gate set. For coherent errors, which include gate overrotation and crosstalk, we demonstrate a reduction of the error scaling in an 𝐿-depth circuit from 𝑂(𝐿) to 𝑂(√𝐿). This asymptotic error suppression behavior can be proven in a regime where all gates, including those constituting the error-suppressing protocol itself, are noisy. Going beyond coherent errors, we derive the general form of decoherence noise that can be suppressed by REAS. Lastly, we experimentally demonstrate the effectiveness of our approach regarding realistic errors using 100-qubit circuits with up to 64 two-qubit gate layers on IBM Quantum processors.
-
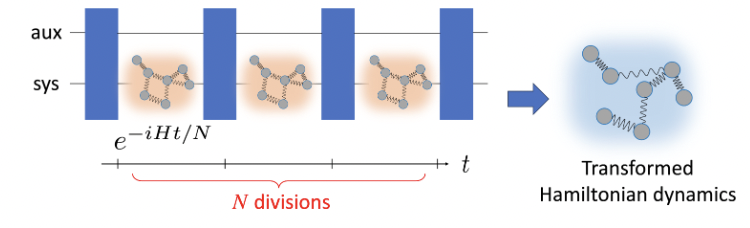 Universal algorithm for transforming Hamiltonian eigenvaluesTatsuki Odake, Hlér Kristjánsson, Philip Taranto, Mio MuraoPhys. Rev. Research 7, 013331 (2025)
Universal algorithm for transforming Hamiltonian eigenvaluesTatsuki Odake, Hlér Kristjánsson, Philip Taranto, Mio MuraoPhys. Rev. Research 7, 013331 (2025)Manipulating Hamiltonians governing physical systems has found a broad range of applications, from quantum chemistry to semiconductor design. In this work, we provide a way of manipulating Hamiltonians, by transforming their eigenvalues while keeping their eigenstates unchanged. We develop a universal algorithm that deterministically implements any desired (suitably differentiable) function on the eigenvalues of any unknown Hamiltonian, whose positive-time and negative-time dynamics are given as a black box. Our algorithm uses correlated randomness to efficiently combine two subroutines—namely controlization and Fourier series simulation—exemplifying a general compilation procedure that we develop. The time complexity of our algorithm is significantly reduced via said compilation technique compared to a naïve concatenation of the subroutines and outperforms similar methods based on the quantum singular value transformation.
-
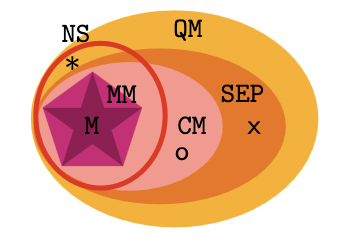 Characterising the Hierarchy of Multi-time Quantum Processes with Classical MemoryPhilip Taranto, Marco Túlio Quintino, Mio Murao, Simon MilzQuantum 8, 1328 (2024)
Characterising the Hierarchy of Multi-time Quantum Processes with Classical MemoryPhilip Taranto, Marco Túlio Quintino, Mio Murao, Simon MilzQuantum 8, 1328 (2024)Memory is the fundamental form of temporal complexity: when present but uncontrollable, it manifests as non-Markovian noise; conversely, if controllable, memory can be a powerful resource for information processing. Memory effects arise from/are transmitted via interactions between a system and its environment; as such, they can be either classical or quantum. From a practical standpoint, quantum processes with classical memory promise near-term applicability: they are more powerful than their memoryless counterpart, yet at the same time can be controlled over significant timeframes without being spoiled by decoherence. However, despite practical and foundational value, apart from simple two-time scenarios, the distinction between quantum and classical memory remains unexplored. Here, we analyse multi-time quantum processes with memory mechanisms that transmit only classical information forward in time. Complementing this analysis, we also study two related – but simpler to characterise – sets of processes that could also be considered to have classical memory from a structural perspective, and demonstrate that these lead to remarkably distinct phenomena in the multi-time setting. Subsequently, we systematically stratify the full hierarchy of memory effects in quantum mechanics, many levels of which collapse in the two-time setting, making our results genuinely multi-time phenomena.
-
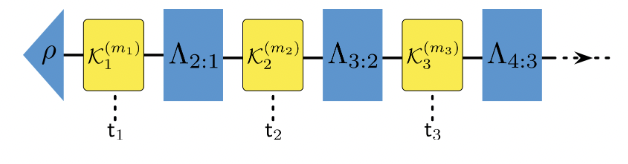
 Hidden Quantum Memory: Is Memory There When Somebody Looks?Philip Taranto, Thomas J. Elliott, Simon MilzQuantum 7, 991 (2023)
Hidden Quantum Memory: Is Memory There When Somebody Looks?Philip Taranto, Thomas J. Elliott, Simon MilzQuantum 7, 991 (2023)In classical physics, memoryless dynamics and Markovian statistics are one and the same. This is not true for quantum dynamics, first and foremost because quantum measurements are invasive. Going beyond measurement invasiveness, here we derive a novel distinction between classical and quantum processes, namely the possibility of hidden quantum memory. While Markovian statistics of classical processes can always be reproduced by a memoryless dynamical model, our main result shows that this is not true in quantum mechanics: We first provide an example of quantum non-Markovianity whose manifestation depends on whether or not a previous measurement is performed – an impossible phenomenon for memoryless dynamics; we then strengthen this result by demonstrating statistics that are Markovian independent of how they are probed, but are nonetheless still incompatible with memoryless quantum dynamics. Thus, we establish the existence of Markovian statistics gathered by probing a quantum process that nevertheless fundamentally require memory for their creation.
-
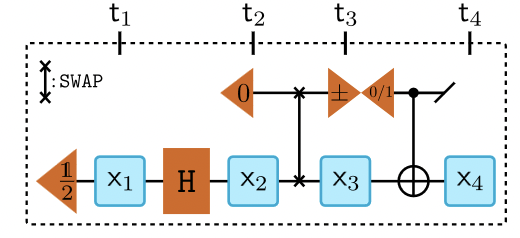
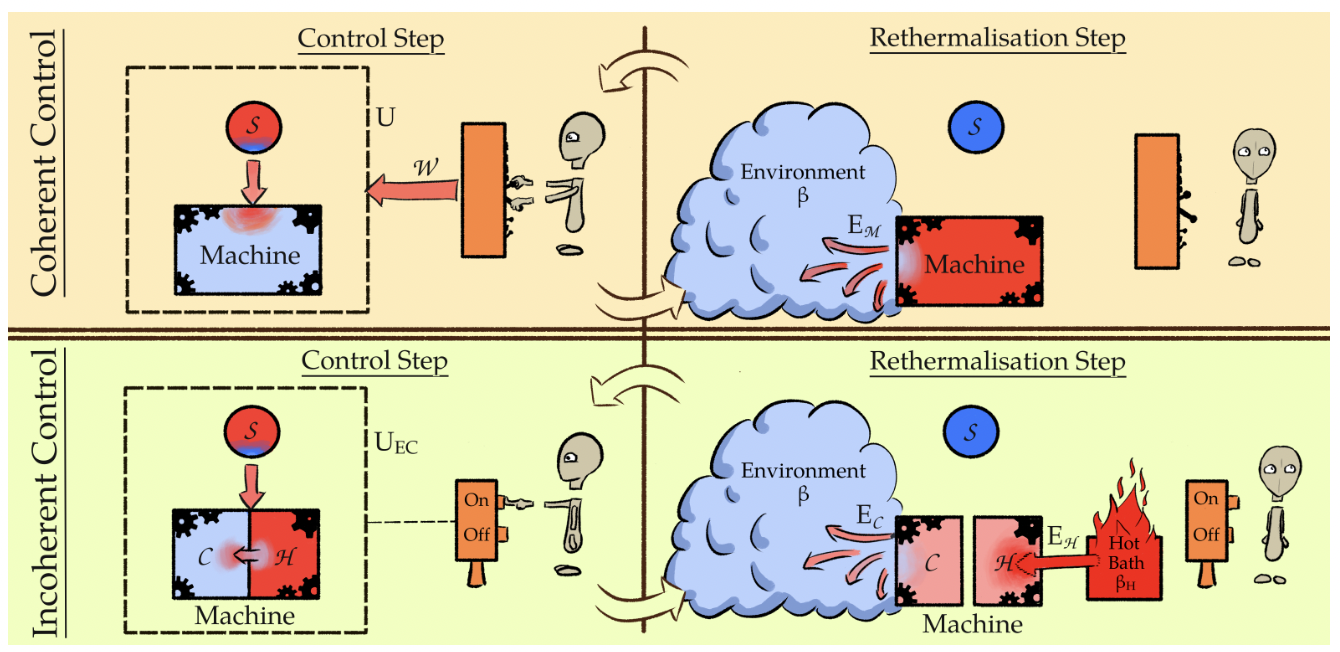 Landauer vs. Nernst: What is the True Cost of Cooling a Quantum System?Philip Taranto, Faraj Bakhshinezhad, Andreas Bluhm, Ralph Silva, Nicolai Friis, Maximilian P. E. Lock, Giuseppe Vitagliano, Felix C. Binder, Tiago Debarba, Emanuel Schwarzhans, Fabien Clivaz, Marcus HuberPRX Quantum 4, 010332 (2023)
Landauer vs. Nernst: What is the True Cost of Cooling a Quantum System?Philip Taranto, Faraj Bakhshinezhad, Andreas Bluhm, Ralph Silva, Nicolai Friis, Maximilian P. E. Lock, Giuseppe Vitagliano, Felix C. Binder, Tiago Debarba, Emanuel Schwarzhans, Fabien Clivaz, Marcus HuberPRX Quantum 4, 010332 (2023)Thermodynamics connects our knowledge of the world to our capability to manipulate and thus to control it. This crucial role of control is exemplified by the third law of thermodynamics, Nernst’s unattainability principle, which states that infinite resources are required to cool a system to absolute zero temperature. But what are these resources and how should they be utilized? And how does this relate to Landauer’s principle that famously connects information and thermodynamics? We answer these questions by providing a framework for identifying the resources that enable the creation of pure quantum states. We show that perfect cooling is possible with Landauer energy cost given infinite time or control complexity. However, such optimal protocols require complex unitaries generated by an external work source. Restricting to unitaries that can be run solely via a heat engine, we derive a novel Carnot-Landauer limit, along with protocols for its saturation. This generalizes Landauer’s principle to a fully thermodynamic setting, leading to a unification with the third law and emphasizes the importance of control in quantum thermodynamics.
-
 Connecting commutativity and classicality for multitime quantum processesFattah Sakuldee, Philip Taranto, Simon MilzPhys. Rev. A 106, 022416 (2022)
Connecting commutativity and classicality for multitime quantum processesFattah Sakuldee, Philip Taranto, Simon MilzPhys. Rev. A 106, 022416 (2022)Understanding the demarcation line between classical and quantum is an important issue in modern physics. The development of such an understanding requires a clear picture of the various concurrent notions of “classicality” in quantum theory presently in use. Here we focus on the relationship between Kolmogorov consistency of measurement statistics—the foundational footing of classical stochastic processes in standard probability theory—and the commutativity (or absence thereof) of measurement operators—a concept at the core of quantum theory. Kolmogorov consistency implies that the statistics of sequential measurements on a (possibly quantum) system could be explained entirely by means of a classical stochastic process, thereby providing an operational notion of classicality. On the other hand, commutativity of measurement operators is a structural property that holds in classical physics and its breakdown is the origin of the uncertainty principle, a fundamentally quantum phenomenon. We formalize the connection between these two a priori independent notions of classicality, demonstrate that they are distinct in general and detail their implications for memoryless multitime quantum processes.
-
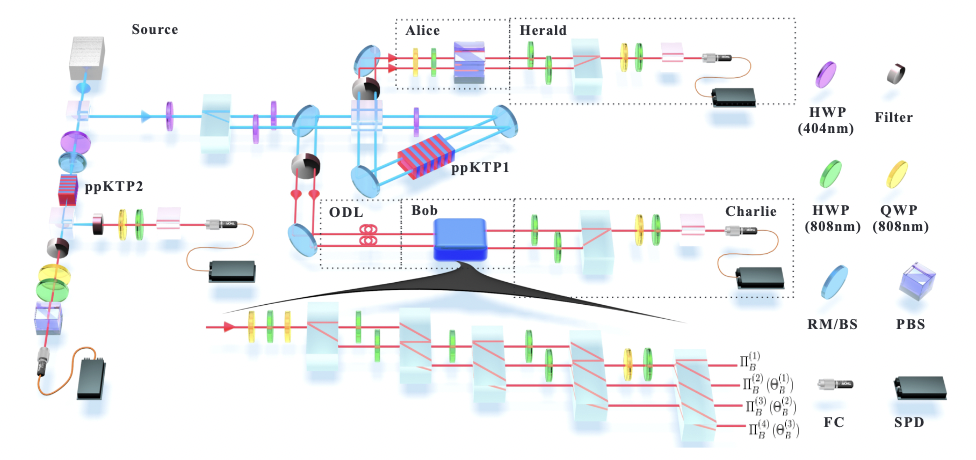 Experimental Demonstration of Instrument-specific Quantum Memory Effects and Non-Markovian Process Recovery for Common-Cause ProcessesYu Guo, Philip Taranto, Bi-Heng Liu, Xiao-Min Hu, Yun-Feng Huang, Chuan-Feng Li, Guang-Can GuoPhys. Rev. Lett. 126, 230401 (2021)
Experimental Demonstration of Instrument-specific Quantum Memory Effects and Non-Markovian Process Recovery for Common-Cause ProcessesYu Guo, Philip Taranto, Bi-Heng Liu, Xiao-Min Hu, Yun-Feng Huang, Chuan-Feng Li, Guang-Can GuoPhys. Rev. Lett. 126, 230401 (2021)The duration, strength, and structure of memory effects are crucial properties of physical evolution. Because of the invasive nature of quantum measurement, such properties must be defined with respect to the probing instruments employed. Here, using a photonic platform, we experimentally demonstrate this necessity via two paradigmatic processes: future-history correlations in the first process can be erased by an intermediate quantum measurement; for the second process, a noisy classical measurement blocks the effect of history. We then apply memory truncation techniques to recover an efficient description that approximates expectation values for multitime observables. Our proof-of-principle analysis paves the way for experiments concerning more general non-Markovian quantum processes and highlights where standard open systems techniques break down.
-
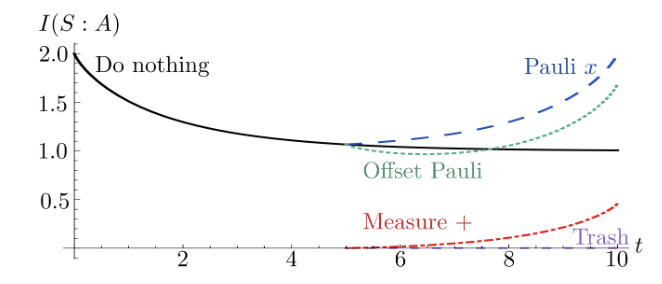 Non-Markovian Memory Strength Bounds Quantum Process RecoverabilityPhilip Taranto, Felix A. Pollock, Kavan Modinpj Quantum Inf. 7, 149 (2021)
Non-Markovian Memory Strength Bounds Quantum Process RecoverabilityPhilip Taranto, Felix A. Pollock, Kavan Modinpj Quantum Inf. 7, 149 (2021)Generic non-Markovian quantum processes have infinitely long memory, implying an exact description that grows exponentially in complexity with observation time. Here, we present a finite memory ansatz that approximates (or recovers) the true process with errors bounded by the strength of the non-Markovian memory. The introduced memory strength is an operational quantity and depends on the way the process is probed. Remarkably, the recovery error is bounded by the smallest memory strength over all possible probing methods. This allows for an unambiguous and efficient description of non-Markovian phenomena, enabling compression and recovery techniques pivotal to near-term technologies. We highlight the implications of our results by analyzing an exactly solvable model to show that memory truncation is possible even in a highly non-Markovian regime.
-
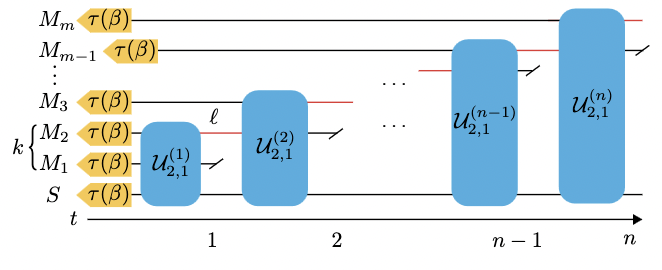 Exponential improvement for quantum cooling through finite-memory effectsPhilip Taranto, Faraj Bakhshinezhad, Philipp Schüttelkopf, Fabien Clivaz, Marcus HuberPhys. Rev. Appl. 14, 054005 (2020)
Exponential improvement for quantum cooling through finite-memory effectsPhilip Taranto, Faraj Bakhshinezhad, Philipp Schüttelkopf, Fabien Clivaz, Marcus HuberPhys. Rev. Appl. 14, 054005 (2020)Practical implementations of quantum technologies require preparation of states with a high degree of purity—or, in thermodynamic terms, very low temperatures. Given finite resources, the third law of thermodynamics prohibits perfect cooling; nonetheless, attainable upper bounds for the asymptotic ground-state population of a system repeatedly interacting with quantum thermal machines have been derived. These bounds apply within a memoryless (Markovian) setting, in which each refrigeration step proceeds independently of those previous. Here, we expand this framework to study the effects of memory on quantum cooling. By introducing a memory mechanism through a generalized collision model that permits a Markovian embedding, we derive achievable bounds that provide an exponential advantage over the memoryless case. For qubits, our bound coincides with that of heat-bath algorithmic cooling, which our framework generalizes to arbitrary dimensions. We lastly describe the adaptive stepwise optimal protocol that outperforms all standard procedures.
-
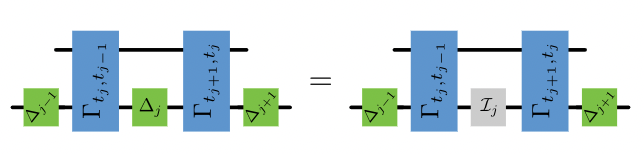 When is a non-Markovian quantum process classical?Simon Milz, Dario Egloff, Philip Taranto, Thomas Theurer, Martin B. Plenio, Andrea Smirne, Susana F. HuelgaPhys. Rev. X 10, 041049 (2020)
When is a non-Markovian quantum process classical?Simon Milz, Dario Egloff, Philip Taranto, Thomas Theurer, Martin B. Plenio, Andrea Smirne, Susana F. HuelgaPhys. Rev. X 10, 041049 (2020)More than a century after the inception of quantum theory, the question of which traits and phenomena are fundamentally quantum remains under debate. Here, we give an answer to this question for temporal processes that are probed sequentially by means of projective measurements of the same observable. Defining classical processes as those that can, in principle, be simulated by means of classical resources only, we fully characterize the set of such processes. Based on this characterization, we show that for non-Markovian processes (i.e., processes with memory), the absence of coherence does not guarantee the classicality of observed phenomena; furthermore, we derive an experimentally and computationally accessible measure for nonclassicality in the presence of memory. We then provide a direct connection between classicality and the vanishing of quantum discord between the evolving system and its environment. Finally, we demonstrate that—in contrast to the memoryless setting—in the non-Markovian case, there exist processes that are genuinely quantum; i.e., they display nonclassical statistics independent of the measurement scheme that is employed to probe them.
-
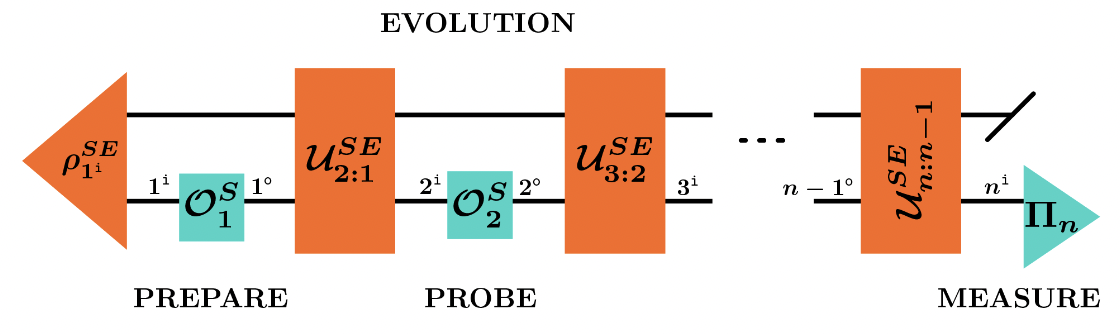 Memory Effects in Quantum ProcessesPhilip TarantoInt. J. Quantum Inf. 18, 1941002 (2020)
Memory Effects in Quantum ProcessesPhilip TarantoInt. J. Quantum Inf. 18, 1941002 (2020)Understanding temporal processes and their correlations in time is of paramount importance for the development of near-term technologies that operate under realistic conditions. Capturing the complete multi-time statistics defining a stochastic process lies at the heart of any proper treatment of memory effects. In this thesis, using a novel framework for the characterisation of quantum stochastic processes, we first solve the long standing question of unambiguously describing the memory length of a quantum processes. This is achieved by constructing a quantum Markov order condition that naturally generalises its classical counterpart for the quantification of finite-length memory effects. As measurements are inherently invasive in quantum mechanics, one has no choice but to define Markov order with respect to the interrogating instruments that are used to probe the process at hand: different memory effects are exhibited depending on how one addresses the system, in contrast to the standard classical setting. We then fully characterise the structural constraints imposed on quantum processes with finite Markov order, shedding light on a variety of memory effects that can arise through various examples. Lastly, we introduce an instrument-specific notion of memory strength that allows for a meaningful quantification of the temporal correlations between the history and the future of a process for a given choice of experimental intervention. These findings are directly relevant to both characterising and exploiting memory effects that persist for a finite duration. In particular, immediate applications range from developing efficient compression and recovery schemes for the description of quantum processes with memory to designing coherent control protocols that efficiently perform information-theoretic tasks, amongst a plethora of others.
-
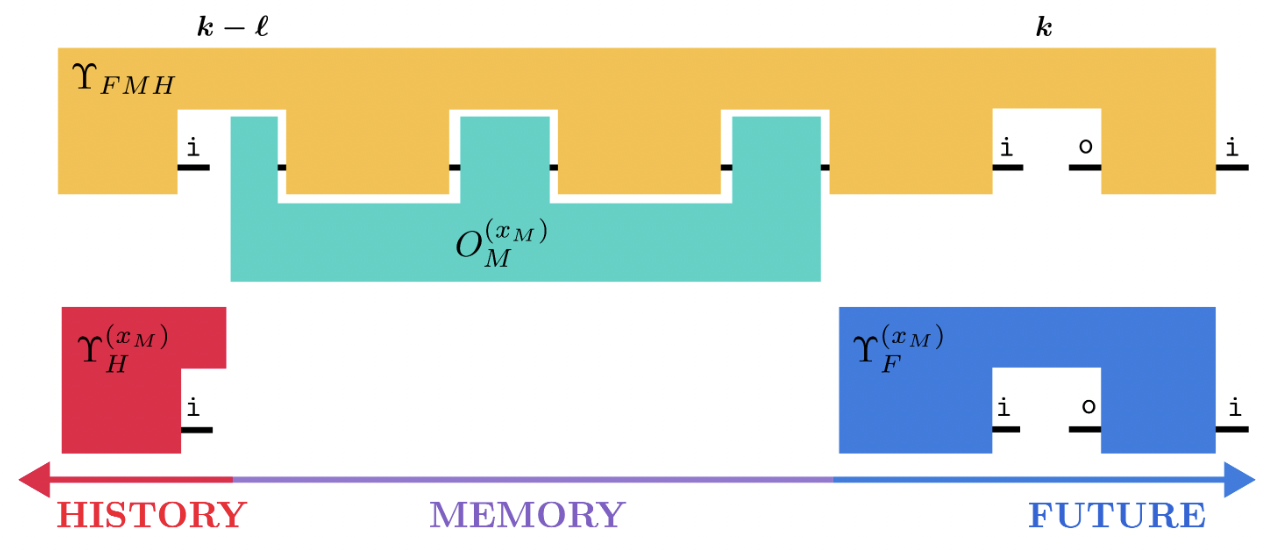 The Structure of Quantum Stochastic Processes with Finite Markov OrderPhilip Taranto, Simon Milz, Felix A. Pollock, Kavan ModiPhys. Rev. A 99, 042108 (2019)
The Structure of Quantum Stochastic Processes with Finite Markov OrderPhilip Taranto, Simon Milz, Felix A. Pollock, Kavan ModiPhys. Rev. A 99, 042108 (2019)Non-Markovian quantum processes exhibit different memory effects when measured in different ways; an unambiguous characterization of memory length requires accounting for the sequence of instruments applied to probe the system dynamics. This instrument-specific notion of quantum Markov order displays stark differences to its classical counterpart. Here, we explore the structure of quantum stochastic processes with finite length memory in detail. We begin by examining a generalized collision model with memory, before framing this instance within the general theory. We detail the constraints that are placed on the underlying system-environment dynamics for a process to exhibit finite Markov order with respect to natural classes of probing instruments, including deterministic (unitary) operations and sequences of generalized quantum measurements with informationally-complete preparations. Lastly, we show how processes with vanishing quantum conditional mutual information form a special case of the theory. Throughout, we provide a number of representative, pedagogical examples to display the salient features of memory effects in quantum processes.
-
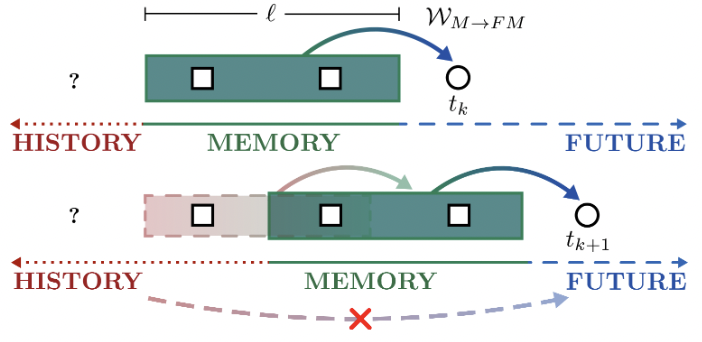 Quantum Markov OrderPhilip Taranto, Felix A. Pollock, Simon Milz, Marco Tomamichel, Kavan ModiPhys. Rev. Lett. 122, 140401 (2019)
Quantum Markov OrderPhilip Taranto, Felix A. Pollock, Simon Milz, Marco Tomamichel, Kavan ModiPhys. Rev. Lett. 122, 140401 (2019)We formally extend the notion of Markov order to open quantum processes by accounting for the instruments used to probe the system of interest at different times. Our description recovers the classical property in the appropriate limit: when the stochastic process is classical and the instruments are noninvasive, i.e., restricted to orthogonal, projective measurements. We then prove that there do not exist non-Markovian quantum processes that have finite Markov order with respect to all possible instruments; the same process exhibits distinct memory effects when probed by different instruments. This naturally leads to a relaxed definition of quantum Markov order with respect to specified instrument sequences. The memory effects captured by different choices of instruments vary dramatically, providing a rich landscape for future exploration.
-
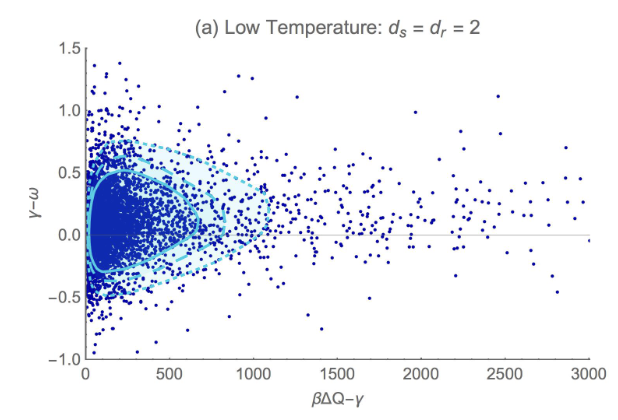 Emergence of a Fluctuation Relation for Heat in Nonequilibrium Open Quantum ProcessesPhilip Taranto, Felix A. Pollock, Kavan ModiPhys. Rev. E 97, 05211 (2018)
Emergence of a Fluctuation Relation for Heat in Nonequilibrium Open Quantum ProcessesPhilip Taranto, Felix A. Pollock, Kavan ModiPhys. Rev. E 97, 05211 (2018)In a generalized framework for the Landauer erasure protocol, we study bounds on the heat dissipated in typical nonequilibrium quantum processes. In contrast to thermodynamic processes, quantum fluctuations are not suppressed in the nonequilibrium regime and cannot be ignored, making such processes difficult to understand and treat. Here we derive an emergent fluctuation relation that virtually guarantees the average heat produced to be dissipated into the reservoir either when the system or reservoir is large (or both) or when the temperature is high. The implication of our result is that for nonequilibrium processes, heat fluctuations away from its average value are suppressed independently of the underlying dynamics exponentially quickly in the dimension of the larger subsystem and linearly in the inverse temperature. We achieve these results by generalizing a concentration of measure relation for subsystem states to the case where the global state is mixed.